確率の連鎖で考える：「ベイズな予測」で未来を拓け（3）

確率を得ているプロセスが予測に重要であることを理解したところで、今度は逆を考えてみよう。カードを裏返すプロセスが、ブランケットでも掛けられたように見えないとしたらどうなるだろう。

[宮谷隆，ITmedia]

　第1回、第2回の記事を読めば、確率を得ているプロセスが予測に非常に重要であることが理解できると思う。今度は逆を考えてみよう。カードを裏返すプロセスがまるでブランケットでも掛けられたように見えないとしたら、どうなるだろう。

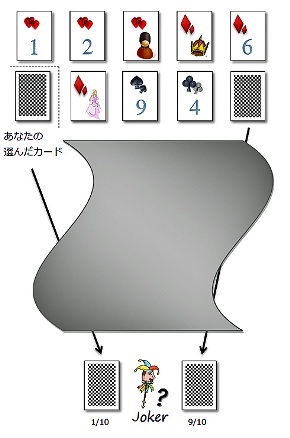
　第2回の記事では、カードゲームでの結果を得た。カードは2枚なのに1/10でアタリとなるカードと9/10でアタリとなるカードが表れる。この結果の違いを生み出している要因は何だろうか。予測ができるということは、裏を返せば何が要因となって結果が出るのかを分析することでもある。

　左図のように、結果が表れる過程が透明なブランケットで覆われていれば理解しやすい。しかし、色つきのブランケットが掛けられていれば、アタリとなる確率が異なる理由は分からない。この場合、過程は分からずじまいだが、要因の違いは認識できる。要因として得ている情報は1つ。2枚になるまでに裏返すカードの数である。

　一般化された状況への適用は、この例ではあまりに単純過ぎる。だが、理解には容易な展開を生む。例えば、最終的に出てきた2枚のカードを、車の購入を検討する2人の顧客や不動産の購入を検討している2人の顧客に置き換えてみればいい。

　このとき、属性は「2枚になるまでに裏返すカードの数」から一変し、一挙に増える。年収、性別、年齢、既婚別、子供の数、通勤距離、趣味、所有する不動産の有無、他に所有する車、地域などのほか、可能な限り多くの情報が入ってくる。さらに、本来は対象にしたいがデータを得られない情報もある。要するに、カードが当たる確率のように綺麗な確率変化の過程を通らないということである。

　さらに言えば、どのカードが1枚目に裏返されるのか、といった順序すら定かではない。購入対象者の確率を変化させるプロセスに、年収が先か、年齢が先かは実際、観察のしようがないのである。だから、このブランケット内の正確な確率過程は知る由もない。ただ、要因と要因との結びつきという膨大な属性の組み合わせをコンピュータが計算し、その中から結果を強く導き出すようなある特定の属性の組み合わせを発見するのである。これは要因分析になり、同時に予測モデルになる。

　さて、ベイジアンは要因分析と予測を使い世界に働きかけができると、第2回の記事で述べた。そこで、総務省統計センターの自治体データ、地域データから見えてくる自治体の姿をベイズ推定してみよう。上記のような予測モデルができれば、今まで気がつかなかった社会傾向や関係性などを抽出できるはずである。

　自治体の総人口を予測するモデルを作成する。「統計でみる都道府県のすがた」というデータで2007年から2009年までのデータを分析する。データ項目は、都道府県名、総人口、男子・女子人口、人口密度、男子・女子死亡率、合計特殊出生率（人口千人に対する出生率）、転入・転出率（転入（出）者数／総人口 ）、核家族世帯の割合、老年人口指数（老年人口／生産年齢人口×100 ）、婚姻率・離婚率などのほか、全部で42の属性を要因として、分析の対象にする。

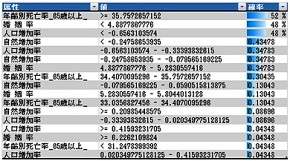
　書籍『ベイズな予測』で紹介している方法で予測モデルを作ると、左図のように、「自然増加率」「婚姻率」「人口増加率」「65歳以上の死亡率」で総人口を予測できる。この時にコンピュータは総人口を5つのセグメントに分けてくれる。総人口が最も少ないとされる地域のセグメントは、169万人以下の人口の地域で、23地域ある。そして、次のような特徴がある。

• 1.65歳以上の方の死亡率が高いこと。（1000人に35人以上）
• 2.婚姻率が低いこと。（1000人に4人以下）
• 3.人口増加率は、-0.6％以下
• 4.自然増加率は、- 0.2％以下

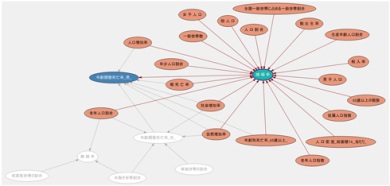
　人口が減り続ければ、自治体は税収も減り、また活力も失われていく。そこで、ベイジアンらしく人口を増減させる要因となる「婚姻率」に着目して、世界に働きかけていく。「婚姻率」が高ければ、人口増加率や自然増加率（出生数と死亡数の差を総人口で割った値）も高くなるという仮説に基づいて予測モデルを作る。この時、「婚姻率」、それと反する「離婚率」、加えて、「男性死亡率」と「女性死亡率」の4つの属性を予測対象にして、ベイジアンネットワークを生成してみた。

　上図から、予測対象にした「婚姻率」（緑の楕円）は非常に多くの属性と関係があることが分かる。これは、予測する際に利用できる属性が多いということである。総面積1平方キロメートルあたりの人口密度や、周りに赤ちゃんを見る機会があるといった出生率、これとは反対に、死亡率や男子人口の差異、65歳以上の人と15歳から64歳までの人が地域にいる比率を表す老年人口指数などが大きく関与していることが分かる。また、65歳以上の親族が同じ地域にいるかどうかも重要な要素だ。

　分析を進めると「自然増加率」と「婚姻率」に強い関係性があることが分かる。ベイズ推定では有効グラフを提供するので、どちらの属性が、どちらの属性に影響を与えるかを示すことができる。ここでは「婚姻率」が「自然増加率」に関わるのではなくて、「自然増加率」が「婚姻率」に関わっていることを見つけられる。また、「婚姻率」と「男性の死亡率」（青い楕円）が相互に影響を与えていることである。

　これに対して「離婚率」は社会的な属性と関係のあるものが少ない。「婚姻率」に比べると、違和感を覚えるくらいだ。興味深いのは、総人口に対する65歳以上の人口比を表す「老年人口割合」が「離婚率」に影響を及ぼしている点である。「離婚率」の高い地域の方が「老年人口割合」が低いのである。

　つまり、離婚の多い地域は、離婚の少ない地域に比べて老人が少ないということが言える。そこで「老年人口割合」に着目すると、面白いことに「婚姻率」と「離婚率」、そして「女性の死亡率」に影響を及ぼしていることが分かる。また、核家族世帯の割合が高い地域の方が「離婚率」が高かったり、地域における「共働き世帯の割合」が高い地域のほうが、「離婚率」が低いということも分かってくる。

　人口増加に影響を与える「男性の死亡率」に関しては、影響を与える要因が比較的多く存在する。寿命という自然の要因以外に、極めて多種多様な要因が男性の生死を決めていることになる。要因としては、「婚姻率」の多い地域に住んでいるのか、住んでいないのかで生死が分かれるという結果も出る。残念ながら、分析データは地域属性を元にしたサマリーなので、それ以上は詳細データを分析しなければならないが、既婚者の多い地域と少ない地域を比べると既婚者の多い地域の男性は長生きするのである。

　婚姻率以外では「人口増加率」、労働人口を示す「社会増加率」「自然増加率」や「女性の死亡率」も「男性の死亡率」に影響を与えている。「女性の死亡率」の影響を受けるというのは非常に面白い。特定の女性と結婚しているか、していないかにかかわらず、女性の死亡率の高い地域に住んでいる男性は一般に死亡率が高いことになる。これは、その地域が一般に死亡率が高いということなのだろうか。そこで「女性の死亡率」に着目すると有効グラフは反対にならないことが分かる。粗死亡率は相関しないのである。

　なんと！男性の生死は女性にはあまり関係がない！

　ということである。この極めて非対称な関係は男性の方が実はデリケートという興味深い考察を生み出す。ほかに、共働き世帯の多い地域ほど女性の死亡率が少ないことも分かる。

　ベイズ推定の結果をまとめると、人口を決定している要因の大きなものは「婚姻率」であること。「婚姻率」と「離婚率」、どちらにも「老年人口割合」が関与していること。「共働き世帯割合」が「離婚率」や女性の死亡要因に関係があることなどである。

　こうした要因を考慮して、地域の環境作りを考えることで地域に働きかけができる。適切な割合で老人が生活する地域（分析の結果からは、割合は多すぎても少なすぎてもいけないことになっている）および共働き世帯の割合が適切な地域は、婚姻率を上昇させて人口増加を期待することができる地域ということになる。従って、女性の働きやすい職場環境の整備と老人が適切な割合で社会に存在する環境を整備することが人口の増加を地域にもたらす。

　ベイズ推定は、物事を確率の連鎖として捉え直してくれる。予測モデルの利用によって、自治体マーケティングや地方のデザインを再考させ、新しい世界を築くための道しるべを示す手段として活用できる。

企業向け情報を集約した「ITmedia エンタープライズ」も併せてチェック

関連ホワイトペーパー

スパム | データマイニング | ブログ

著者プロフィール：宮谷 隆（みやたに　たかし）

マイクロソフト株式会社　シニア　テクニカルアーキテクト。日本シリコングラフィックスにて、データマイニング製品MineSetのエンジニア兼プロダクトマネージャを務め、要因分析や予測販売などのソリューションを提供した。マイクロソフトでは、現在のクラウドコンピューティングの先駆けとなった「Hailstorm」の啓発活動を2001年から展開、.NET FrameworkやSQL Server のデータマイニング機能をはじめ、RFIDなど最新技術の啓発活動を行ってきた。現在は、主にWindows Azureを使ったクラウドコンピューティングの啓発活動を推進している。また、政府向けに経済産業省や総務省の協議会における技術標準策定に関わっている。